Lineare Regression kurz und knapp:
- Die lineare Regression ist eine Gerade, die Werte vorhersagt
- Abhängig von den Daten wird der bestmögliche Durchschnitt für jeden Zeitpunkt berechnet und in einer Linie dargestellt
Die lineare Regression ist eine Linie, die durch ein Streudiagramm geht. Anhand dieser Linie können wir Werte vorhersagen. Wie der Name sagt ist diese Gerade linear. Es ist also eine lineare Funktion wie man sie aus der 8. Klasse kennt – nur mit anderen Buchstaben:
\hat{y}_i = \beta_0 + \beta_1x_{i1}+\epsilon_i
- \hat{y}_i = Eine Y-Koordinate auf der Geraden (z.B. Wohnpreis)
- x_i = Die X-Koordinate, die die Y-Koordinate berechnet (z.B. m²-Wohnfläche)
- i = Das kleine i steht für das Objekt, das wir beobachten (z.B. die Dachgeschosswohnung in der Beispielstraße 42).
- \beta_0 = Die Verschiebung auf der Y-Achse. Je größer \beta_0 ist, desto mehr verschiebt sich die gesamte Funktion der Y-Achse entlang nach oben. (Z.B. der Grundpreis für Wohnungen in Berlin betrage \beta_0 = 20.000€)
- \beta_1 = Die Steigung. Wird \beta_1 größer, wird die Funktion steiler. Ist \beta_1 = 0, ist die Funktion waagerecht. Ist \beta_1 negativ, geht die Gerade bergab. (Z.B. jeder Quadratmeter erhöht den Preis um 1.000€)
\text{Preis}_i = \beta_0 + \beta_1*\text{Wohnfläche}_{i1}+\epsilon_i
Ziel der Regression ist es, die Variablen \beta_0 und \beta_1 bestmöglich zu schätzen. Die Methode dafür nennt sich Kleinste-Quadrate Schätzung.Kleinste-Quadrate Methode
Die Grundformel für die Kleinste-Quadrate (KQ) Methode ist:
\displaystyle\text{KQ} = \sum_{i=1}^{n}{(y_i\thinspace-\thinspace\hat{y}_i)^2}
y_i: Die wahren Y-Werte aus der Punktwolke
\hat{y}_i: Die Y-Schätzwerte auf der linearen Regression
Mit der KQ-Methode berechnen eine Summe aus allen Abständen zwischen unseren echten Y-Werten (y_i – roter Punkt) und der Schätzung unserer linearen Regression (\hat{y}_i – grüner Punkt) und quadrieren diese Abstände (blaue Linie). Wir quadrieren um negative Abstände positiv zu machen und um den Einfluss von großen Fehleinschätzungen zu verstärken.
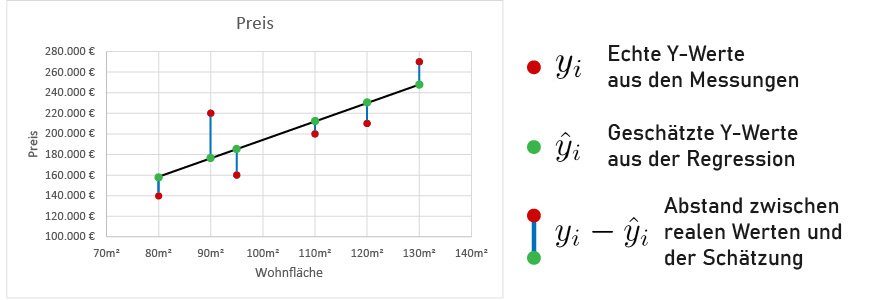
Wir können aber die Gerade auf verschiedene Arten und Weisen mitten in die Punktwolke positionieren. Dadurch verändern sich die Abstände zu den Punkten:
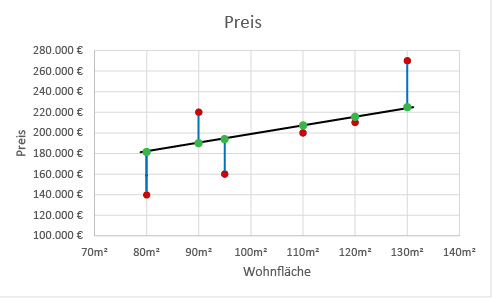
Das Ziel der linearen Regression ist, die gesamte Strecke aller quadrierten blauen Linien so klein wie möglich zu halten. Darum heißt diese Methode auch Kleinste-Quadrate Methode.
Lineare Regression in Python (Jupyter)
Wir importieren als erstes die Pandas Bibliothek, damit wir eine CSV Datei (= Datentabelle) einlesen können:
import pandas as pd Wir erstellen ein Data Frame und befüllen es mit der read_csv Funktion aus Pandas mit der Datei wohnungen.csv:
df = pd.read_csv('wohnungen.csv') Damit wir die Daten visualisiert vor uns haben, brauchen wir eine Funktion aus Matplotlib:
%matplotlib inline
import matplotlib.pyplot as plt Die Funktion heißt scatter(), womit wir ein Streudiagramm
(eng. Scatter Plot) erstellen können. Wir wählen aus, dass die X-Achse die
Wohnfläche ist und die Y-Achse der Preis :
plt.scatter(df['Wohnfläche'], df['Preis'])
plt.show()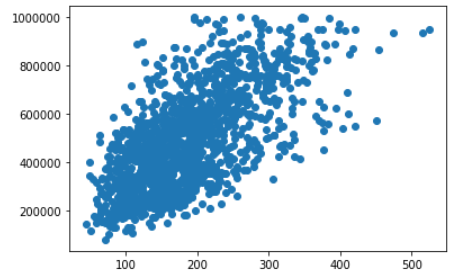 
Durch diese Punktwolke möchten wir jetzt eine lineare Regression ziehen. Dafür brauchen wir die Bibliothek scikit-learn:
from sklearn.linear_model import LinearRegression Die neue Variable linModell übernimmt die Klasse LinearRegression(). Mit der Fit()-Methode passen wir unsere Daten unserem Modell an. Der erste Wert in der Klammer bildet die X-Achse und der zweite Wert die Y-Achse.
linModell = LinearRegression()
linModell.fit(df[['Wohnfläche']],df[['Preis']]) Das ist alles was wir brauchen. Um die mathematische Formel zu bilden, können wir die Verschiebung auf der Y-Achse (auch Intercept genannt) und die Steigung (Coefficient) ausgeben:
print(linModell.intercept_)
print(linModell.coef_) Die Gesamtformel ist also: Preis = Intercept + Coef * Wohnfläche. In der Bibliothek haben wir dafür aber eine vorgefertigte Funktion. Darin geben wir nur die Wohnfläche (X-Wert) ein:
linModell.predict([[x]]) Da visuell alles schöner ist, stellen wir es als Graphen dar:
plt.scatter(df['Wohnfläche'], df['Preis'])
plt.plot([0,500], linModell.predict([[0], [500]]), color = 'red')
plt.show()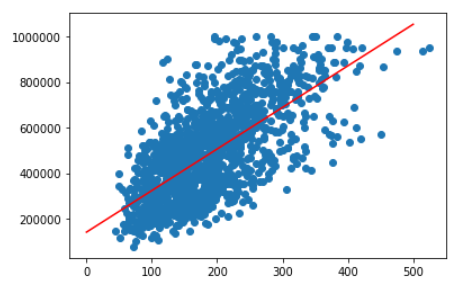 
Lineare Regression mit mehreren Variablen
Meistens muss man aber mehr als eine Variable analysieren, um Werte vorherzusagen. Viele Badezimmer sind beliebt und wirken sich damit auch positiv auf den Preis aus. Ebenso ob die Wohnung bisher saniert wurde oder nicht. Wie nehmen wir also weitere Variablen in die lineare Regression auf? Mathematisch ist es simpel. Wir nehmen einfach nur \beta x für jede Variable auf:
\hat{y}_i = \beta_0 + \beta_1x_{i1} + \beta_2x_{i2} + … + \epsilon_i
Es können beliebig viele … + \beta x + … angehangen werden für verschiedene Variablen.
Modellannahmen
Spoileralarm: Man sollte nicht immer lineare Regressionen verwenden. Welche Voraussetzungen müssen wir aber erfüllen, damit eine lineare Regression sinnvoll ist? Dafür existiert das Gauß-Markov-Theorem. Darin werden sechs Grundannahmen angeführt. Je mehr die Annahmen zutreffen, umso eher ist der Kleinste-Quadrate Schätzer der beste Schätzer für unser Regressionsmodell.
Linearer Zusammenhang
Wie der Name sagt, sollte ein linearer Zusammenhang herrschen. Steigende Wohnungspreise mit steigender Quadratmeteranzahl sind dafür ein gutes Beispiel. Dagegen wäre eine lineare Regression unsinnig, wenn man die Körperkraft mit dem Alter korrelieren lässt. Als Kind und im hohen Alter hat man deutlich weniger Kraft als im körperlichen Hochpunkt zwischen 20-40 Jahren.
Keine Multikollinearität
Kompliziertes Wort. Im Grunde bedeutet es nur, dass die erklärenden Variablen zu sehr untereinander korreliert sind.
Ein Beispiel hierfür ist die Körpergröße und das Körpergewicht. Mit steigender Körpergröße steigt in der Regel auch das Körpergewicht. Das heißt ein kleiner, erklärender Teil dieser Variablen sagt dasselbe aus. Allerdings wird dieser Teil 2x in die Analyse gezogen – einmal vom Körpergewicht und einmal von der Körpergröße. Man kann durch die Überschneidung der beiden Variablen schlecht zuordnen, welche der beiden erklärenden Variablen das Ergebnis wie stark beeinflussen.
Multikollinearität kann man mit einer Korrelationsmatrix, der Toleranz (1 – R-Quadrat) < 0,2 oder einem Varianzinflationsfaktor (1 / Toleranz) > 10 identifizieren.
Erwartungswert der Fehler ist Null
Der Erwartungswert der Fehler in einer linearen Regression ist die Summe der Abstände zwischen Schätzwerten und den wahren Werten. Bei der linearen Regression gehen wir davon aus, dass die Summe all dieser Abstände gleich Null ist.
Sonst könnten wir eine Linie zufällig irgendwie in die Punktwolke legen und sagen, es sei eine lineare Regression. Damit hätte man aber ein verzerrtes Ergebnis und könnte sich die Prognose so zurechtlegen, wie man es gerne hätte.
Homoskedastizität
Wieder ein schwieriges Wort mit einfacher Bedeutung: Homoskedastizität bedeutet, dass die Streuung nicht nach und nach wächst. Das würde passieren, wenn der Fehler mit der erklärenden Variablen mitwächst.
Das passiert z.B. bei Gehaltserhöhungen. Je länger man berufstätig ist, umso eher hängt die Gehaltserhöhung von mehr Faktoren ab. Als Berufseinsteiger hat man relativ wenig Verhandlungsspielraum, während jemand nach 10 Jahren im Berufsleben zwischen 0 bis hin zu sechsstelligen Bereichen mehr auf sein Gehalt bekommen kann. Das wäre heteroskedastisch und würde sich negativ auf die Anwendung der Kleinste-Quadrate-Methode auswirken.
Um zu überprüfen, ob Heteroskedastizität vorliegt, nutzt man den White- oder Levene-Test.
Keine Autokorrelation
Autokorrelation tritt auf, wenn die Fehler voneinander abhängig sind. Es gibt in der Regel zwei Gründe für Autokorrelation:
1. Relevante erklärende Variablen wurden ausgelassen
Wenn inhaltlich relevante, erklärende Variablen ausgelassen werden, fehlt eine wichtige Information, die unser Modell besser erklärt.
Wenn wir den Aktienkurs der DataMines AG anschauen, stellen wir fest, dass wir ein zyklisches Muster haben. Die Punkte hängen also immer vom vorherigen Punkt ab. Um das zu bereinigen, nehmen wir als weitere Variable den Kurs vom DAX, um unseren Aktienpreis zu erklären. Da der DAX genauso ein zyklisches Verhalten aufweist, wird unser Aktienpreis damit erklärt und die Autokorrelation würde verschwinden.
2. Die Funktionsform ist schlecht gewählt
Wir können quadratische Zusammenhänge (z.B. Körperkraft im Verlauf des Alters) nicht linear erklären. Die Körperkraft ist autokorreliert. Man bräuchte also sowohl das Alter als erklärende Variable als auch das quadrierte Alter, um die Autokorrelation auszubessern. Es ist häufig notwendig die Dimension der Variablen zu normalisieren.
2Kommentare
Dr. Heiko Franke
Didaktisch sehr gut aufbereitet, ohne wohnungen.csv jedoch kaum brauchbar, schade ….
Yosef Aziz, Gründer von datamines.de
Hallo Herr Dr. Franke,
vielen Dank für das hilfreiche Feedback! Ich habe die CSV zum Download verlinkt.
Beste Grüße
Yosef