Konfusionsmatrix kurz und knapp:
Die Konfusionsmatrix überprüft, ob die Prognose einer Klassifikation richtiger-/fälschlicherweise wahr oder falsch ist.
- True Positives: Positives Ergebnis vorhergesagt; Positives wahres Ergebnis
- False Positives: Positives Ergebnis vorhergesagt; Negatives wahres Ergebnis
- True Negatives: Negativ Ergebnis vorhergesagt; Negatives wahres Ergebnis
- False Negatives: Negatives Ergebnis vorhergesagt; Positives wahres Ergebnis
Wir bauen ein Machine Learning Modell, das klassifiziert, ob ein Patient einen Tumor hat. Es gibt also nur zwei Zustände:
- Patient hat einen Tumor
- Patient hat keinen Tumor
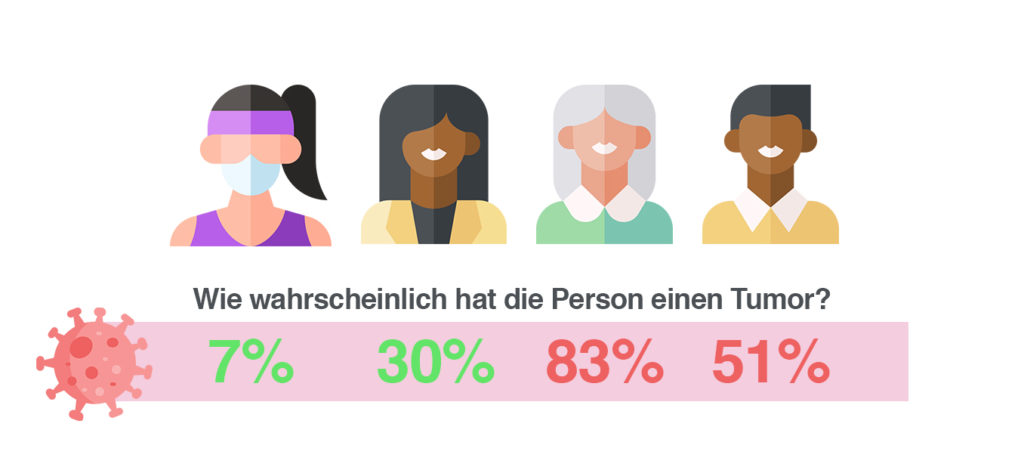
Das Modell ist programmiert, wurde mit sehr vielen Daten gefüttert und ist jetzt bereit zum Einsatz. Bei einer Wahrscheinlichkeit unter 50% sagt das Modell vorher, dass die Testperson keinen Tumor hat. Bei über 50-prozentiger Sicherheit wird ein Tumor identifiziert. Unsere vier Testpersonen werden jetzt mit dem Modell getestet.
- Die Sportlerin: Hat zu 7% einen Tumor
- Die 25-jährige Verkäuferin: Hat zu 30% einen Tumor
- Die 80-jährige Großmutter: Hat zu 83% einen Tumor
- Der 30-jährige Basketballspieler mit vielen Personen in der Familie, die Krebs haben: Hat zu 51% einen Tumor
Die Sportlerin und Verkäuferin haben laut dem Modell keinen Krebs. Die Großmutter und der Basketballspieler werden mit Krebs identifiziert.
Was ist eine Konfusionsmatrix?
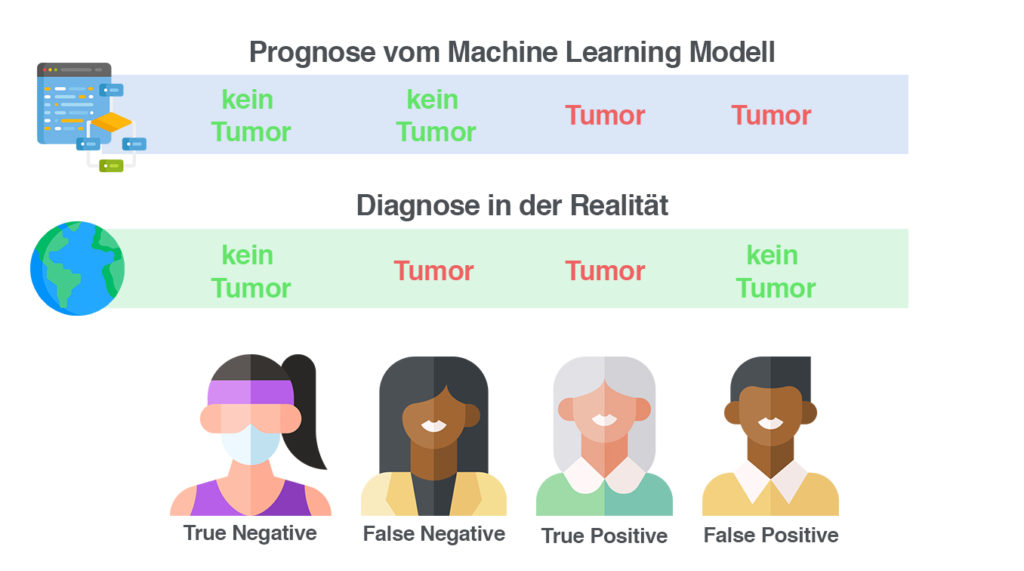
Da Modelle selten perfekt sind, machen sie Fehler. Alle unsere Testpersonen entscheiden sich danach trotzdem noch zum Arzt zu gehen.
Bei der Sportlerin und der Großmutter stellt sich raus, dass die Prognose richtig war.
Bei der Verkäuferin hingegen wurde gesagt, dass sie keinen Krebs hat. Das hat sich als falsch herausgestellt, der Arzt konnte einen Tumor finden.
Beim Basketballspieler das exakte Gegenteil. Das Modell hat einen Tumor erkannt, den es gar nicht gab.
Diese richtigen und falschen Möglichkeiten können in einer Konfusionsmatrix abgebildet werden. Dort wird die Prognose mit der Realität verglichen:
| Wahre Klasse | ||
+ | – | ||
Vorhergesagte Klasse | + | True Positives | False Positives |
– | False Negatives | True Negatives | |
Schätzen wir bei einem Patienten richtigerweise einen Tumor, ist es ein True Positive.
Schätzen wir bei einem Patienten fälschlicherweise einen Tumor, ist es ein False Positive.
Schätzen wir bei einem Patienten richtigerweise keinen Tumor, ist es ein True Negative.
Schätzen wir bei einem Patienten fälschlicherweise keinen Tumor, ist es ein False Negative.
Anwendung in der Praxis - Interpretation der Werte
Abhängig vom Fall ist es unterschiedlich wichtig einen dieser Werte möglichst klein zu halten. Bei Krankheiten ist es besser, mehr Personen fälschlicherweise positiv zu diagnostizieren, um möglichst wenige fälschlicherweise negativ zu diagnostizieren. Um eine optimale Lösung zu finden, müssen wir alle Möglichkeiten kennen, um solche Daten auszuwerten.
Sensitivität
Sensitivität ist die True-Positive-Rate (richtig klassifizierte Positive / Anzahl aller Positiven)
- TP / (TP + FN)
Spezifizität
Spezifizität ist die True-Negative-Rate (richtig klassifizierte Negative / Anzahl aller Negativen)
- TN / (TN + FP)
Präzision
Präzision ist die Rate der richtigerweise positiv Klassifizierten (richtig klassifizierte Positive / Anzahl aller positiv Klassifizierten)
- TP / (TP + FP)
Genauigkeit
Genauigkeit ist die Rate der prozentual richtig Klassifizierten (richtig Klassifizierte / alle Klassifizierungen)
- (TP + TN) / (TP + TN + FP + FN)
Fehlerrate
Fehlerrate ist die Rate der prozentual falsch Klassifizierten (falsch Klassifizierte / alle Klassifizierungen)
- (FP + FN) / (TP + TN + FP + FN)
Wie man eine Grenze für die Klassifikation setzt
Um bei einer Klassifikation zu entscheiden, ab welcher Wahrscheinlichkeit die abhängige Variable zu trifft, müssen wir einen Grenzwert festlegen. Bei wieviel Prozent Sicherheit, erkennt ein Algorithmus aber, dass der Patient einen bösartigen Tumor hat?
Theoretisch setzt man diesen Wert auf 50%. Ist er drüber, wird Tumor als bösartig eingestuft, liegt er bei unter 50%, ist er gutartig. Aber das ist ein zu großes Risiko für den Patienten. Daher müssen verschiedene Grenzwerte getestet werden.
Receiver Operating Characteristics (ROC-Kurve)
Für eine graphische Übersicht erstellt man in der Regel eine ROC Kurve. ROC steht für Receiver Operating Characteristics und es fasst die Konfusionsmatrizen von jedem Grenzwert zusammen.
Auf der X-Achse befindet sich die False-Positive-Rate und auf der Y-Achse die True-Positive-Rate (Sensitivität). Je näher die Punkte am Punkt P(0|1) sind, desto besser ist das Ergebnis. Der Bereich unter der Kurve (AUC = Area Under Curve) ermöglicht uns einen Vergleich zwischen verschiedenen Machine-Learning Modellen. Je größer der Bereich unter der Kurve, desto besser.