Logistische Regression kurz und knapp:
Die logistische Regression sagt vorher, wie wahrscheinlich eines von zwei Ergebnissen bei einer Klassifikation eintreffen wird.
Die logistische Regression wird häufig für Ja/Nein-Fragen verwendet. Dafür gibt es sehr viele Beispiele:
- Ist die erhaltene E-Mail Spam?
- Ist eine Stelle auf einem MRT ein Tumor?
- Ist die Kreditkartentransaktion betrügerisch?
- Wird der Kunde das Auto kaufen?
- Wird der Versicherungsnehmer mehr kosten als er der Versicherung einbringt?
All diese Fragen lassen sich über verschiedene Variablen erklären. Wir können also genauso wie bei der linearen Regression eine Formel verwenden, die aus mehreren erklärenden Variablen besteht.
Lineare vs. Logistische Regression
Zuerst ein kurzer Exkurs in die lineare Regression. Mit der linearen Regression können wir Zahlenwerte vorhersagen. Ein Beispiel ist die Vorhersage des Wohnungspreises anhand der Quadratmeteranzahl. Je mehr Quadratmeter, desto teurer die Wohnung.
Damit können wir aber nicht vorhersagen, ob jemand eine Wohnung kaufen würde. Die lineare Regression kann keine Ja/Nein-Fragen abdecken.
Um vorherzusagen, ob jemand die Wohnung kaufen würde oder nicht, brauchen wir ein Ergebnis zwischen 0 (0% Ja, was bedeutet die Person kauft die Wohnung definitiv nicht) und 1 (100% Ja). Das ist die Kaufwahrscheinlichkeit. Ab >0,5 ist es wahrscheinlicher, dass der Kunde die Wohnung kauft. Das kann man mit der logistischen Regression lösen.
Anwendung der logistischen Regression
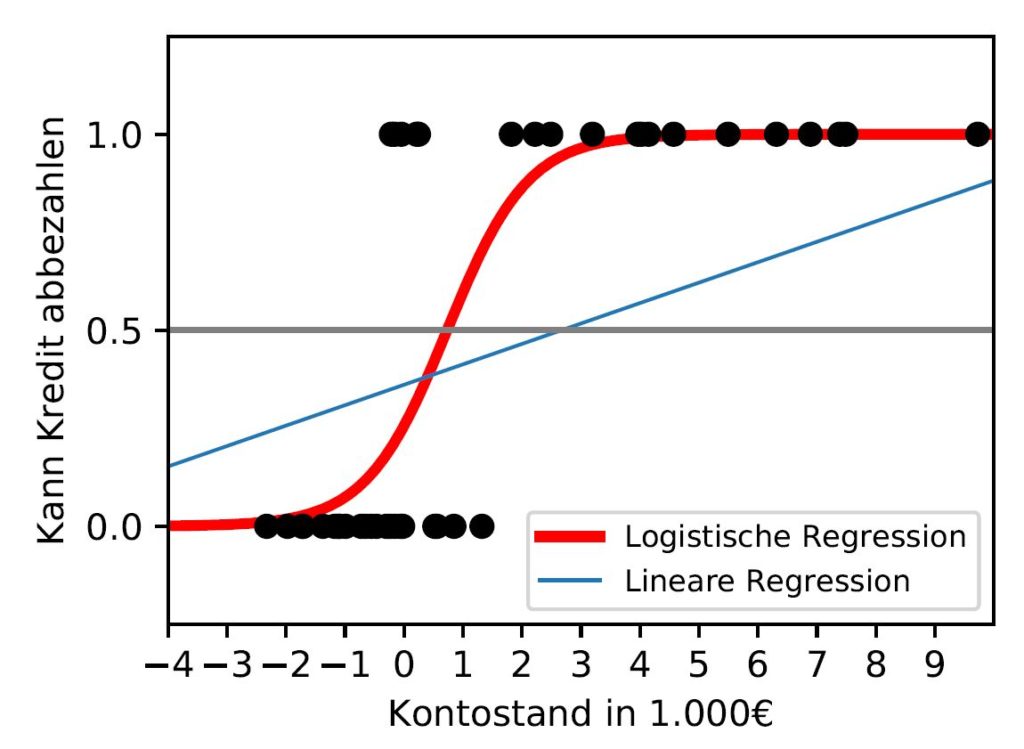
Auf dem Graphen sieht man auf der Y-Achse die Wahrscheinlichkeit, ob Personen einen Kredit zurückbezahlen können. 1.0 = Kann den Kredit mit einer Wahrscheinlichkeit von 100% zurückzahlen, 0.5 = Kann den Kredit mit einer Wahrscheinlichkeit von 50% zurückzahlen, 0.0 = 0%.
Auf der X-Achse findet man den aktuellen Kontostand der Person in 1000€ Schritten. D.h. -4 bedeutet -4000€ Schulden, 9 = 9000€ Überschuss auf dem Konto.
Die einzelnen Punkte auf der Waagerechten von 0.0 und 1.0 sind unsere Datenpunkte. Jeder Punkt steht für eine Person. Bei 0.0 sind alle Personen, die den Kredit nicht zurückzahlen konnten und bei 1.0 alle, die den Kredit zurückgezahlt haben.
Wie man auf dem Bild sieht, ist es nicht sinnvoll eine lineare Regression (blaue Linie) zu benutzen, weil wir irgendwann auf Ergebnisse größer als 1 oder kleiner als 0 stoßen. Da wir Wahrscheinlichkeiten berechnen, ist das nichtssagend. Die rote S-Kurve (Sigmoid-Funktion) hingegen sagt uns, ab welchem x-Wert wir welche Wahrscheinlichkeit zwischen 0 und 1 haben. In diesem Beispielfall liegt die Wahrscheinlichkeit bei einem Kontostand von ca. 1000€ einen Kredit abbezahlen zu können bei 50%.
Logistische Regression mathematisch betrachtet
Lineare Regression zu logistischer Regression umwandeln
Eins haben die lineare- und logistische Regression gemeinsam. Man kann die lineare Regression zur logistischen umwandeln. Die Gerade aus der linearen Funktion soll also zu einer S-Kurve umgewandelt werden, bei der nur Ergebnisse zwischen 0 und 1 erlaubt sind.
Dafür nehmen wir die Formel der linearen Regression:
\hat{y}_i = \beta_0 + \beta_1x_{i1}
- \hat{y}_i = Eine Y-Koordinate auf der Geraden (Kann Kredit abbezahlen)
- x_i = Die X-Koordinate, die die Y-Koordinate berechnet (Kontostand)
- i = Das kleine i steht für das Objekt, das wir beobachten (der konkrete Kontostand von Max Mustermann).
- \beta_0 = Die Verschiebung auf der Y-Achse. Je größer \beta_0 ist, desto mehr verschiebt sich die gesamte Funktion der Y-Achse entlang nach oben. (z.B. häufigerer Ausfall (= negativer Wert) weil Privatpersonen, die Konsumkredite aufnehmen schlechter mit Geld umgehen können)
- \beta_1 = Die Steigung. Wird \beta_1 größer, wird die Funktion steiler. Ist \beta_1 = 0, ist die Funktion waagerecht. Ist \beta_1 negativ, geht die Gerade bergab. (jeder Euro mehr auf dem Konto erhöht die Wahrscheinlichkeit den Kredit abzubezahlen)
Dann setzen wir sie in die sogenannte Sigmoid-Funktion ein. Die Sigmoid-Funktion wandelt die Ergebnisse so um, dass nur ein Ergebnis zwischen 0 und 1 herauskommen kann.
P(Y=1) = \frac{1}{1+\exp(-y)}-y ist die lineare Regression, nur mit umgekehrten Vorzeichen.
P(Y=1) = \frac{1}{1+\exp(-(\beta_0 + \beta_1x))}
Nachdem man die Formel umstellt und zusammenfasst, erhält man am Ende folgende Form
\log(\frac{P(Y=1)}{1-P(Y=1)}) = \beta_0 + \beta_1xDadurch dass die Kurve der logistischen Regression eine Steigung hat, die sich stetig verändert, ist der Einfluss einer erklärenden Variablen an jedem Punkt anders. Die Steigung des Kurvenverlaufs ist erst schwach, dann stark und dann wieder schwach. Dementsprechend ändert sich auch der Einfluss einer jeden erklärenden Variable. Wir können also nicht sagen, dass die Wahrscheinlichkeit um \beta_1 steigt, wenn x_1 um 1 steigt, wie es bei der linearen Regression der Fall ist. Um aber den Einfluss von einzelnen erklärenden Variablen zu analysieren kann man mit Odds arbeiten. Ich erkläre erstmal die theoretischen Grundlagen und erkläre dann, wie man sie in der logistischen Regression anwendet.
Odds
Aus der Formel für die logistische Regression erhalten wir die Formel für logarithmierte Odds:
\log(\frac{P(Y=1)}{1-P(Y=1)})
Odds sind ähnlich wie Wahrscheinlichkeiten. Bei Wahrscheinlichkeiten teilen wir die Anzahl der Erfolge durch die Anzahl der Versuche. Wenn wir also eine 6 würfeln möchten, wäre das eine Wahrscheinlichkeit von \frac{1}{6}.
Bei Odds teilen wir die Anzahl der Erfolge durch die Anzahl der Misserfolge (also alle Ergebnisse von 1 bis 5): \frac{1}{5}. Odds sind also die Anzahl der Erfolge pro Misserfolg. Wir haben also 0,2 Erfolge pro Misserfolg beim Würfeln. Gleiche Odds sind 1 (Münzwurf 1:1), gleiche Wahrscheinlichkeiten sind 0,5 (Münzwurf \frac{1}{2}).
Odds-Ratios
Die Odds Ratios geben einen konstanten Effekt einer erklärenden Variablen (X) wieder. Wie bereits beschrieben konnten wir keinen konstanten Effekt durch \beta_1 herausfinden, weil die Steigung sich immer ändert. Ein konstanter Wert hingegen ermöglicht die Interpretation des logistischen Regressionsmodells.
Odds Ratios von 1,05 geben uns an, dass die Odds an jeder Stelle von X um 5% steigen. Die Differenz der Wahrscheinlichkeiten an zwei Stellen von X sind aber jedes Mal unterschiedlich. Wir messen damit zwar leider nicht den direkten Effekt von X auf Y, aber um wie viel sich die Odds vervielfachen, dass Y eintrifft, wenn X um 1 wächst.
Beispiel: Die Odds, dass ein Mann beim Führerschein besteht liegt bei 1:2 (also eine Wahrscheinlichkeit von \frac{1}{3}). Die Odds, dass eine Frau besteht, sei 5x so groß mit Odds von 5:2 (also eine Wahrscheinlichkeit von \frac{5}{7}). Für alle 10 Männer die bestehen, fallen 20 durch. Für alle 10 Frauen, die bestehen, fallen 4 durch.
Für die Odds Ratios teilt man die Odds, dass eine Frau besteht, durch die Odds, dass ein Mann besteht.
\frac{odds_{weiblich}}{odds_{männlich}}= \frac{\frac{5}{7}}{\frac{1}{3}} = 2,14 = odds\>ratioIn diesem Fall steigen die Odds, die Führerscheinprüfung zu bestehen um 214% wenn man eine Frau ist.
Die Odds Ratio kann man aber auch mittels der logistischen Regression für jede erklärende Variable berechnen. Dafür nehmen wir die Formel der logistischen Regression und teilen sie durch sich selbst. Nur den X-Wert im Zähler verändern wir. Diesen addieren wir mit 1, damit wir analysieren können, welchen Einfluss es hat, wenn X um 1 wächst.
\frac{odds_{x_j+1}}{odds_{x_j}} = \frac{exp(\beta_0+\beta_1(x_1)+…\beta_j(x_j+1)+…)}{exp(\beta_0+\beta_1(x_1)+…\beta_jx_j+…)}Nachdem man den ganzen Term kürzt, kommt man auf
\frac{odds_{x_j+1}}{odds_{x_j}} = exp(\beta_j)Das Odds Ratio für logistische Regressionen ist also die eulersche Zahl hoch dem jeweiligen Beta.
Interpretation der logistischen Regression
Mit der logistischen Regression können wir also die Wahrscheinlichkeit bestimmen, wie sich der y-Wert verhält, wenn der x-Wert wächst.
Mit Hilfe der Betas können wir Odd Ratios herausfinden, indem wir das jeweilige Beta in die e-Funktion einsetzen. Damit erhält man den Einfluss auf die Odds, wenn der X-Wert um 1 wächst.
Beispiel: E-Mail Spam-Erkennung
Wir entwickeln ein Modell, das E-Mails mithilfe der logistischen Regression als Spam einordnen soll. Um es simpel zu halten, betrachten wir als erklärende Variablen nur die Anzahl an Rechtschreibfehlern und ob die E-Mail den Text „SIE HABEN GEWONNEN“ enthält.
| Erklärende Variable | Beta | Odds Ratio |
| Intercept | -3,2 | 0,04 |
| Anzahl an Rechtschreibfehlern | 1,3 | 3,7 |
| Enthält „SIE HABEN GEWONNEN“ (ja/nein) | 2,1 | 8,17 |
Interpretation des Intercepts: Der Interceptwert liefert uns die logarithmierten Odds, wenn alle anderen Variablen 0 sind. Es liefert keine wertvollen Informationen, aber ohne das Intercept wäre das Modell verzerrt.
Interpretation der metrischen Variablen (Anzahl an Rechtschreibfehlern): Pro Rechtschreibfehler erhöhen sich die Odds von Spam vs. Kein Spam um 370%, wenn alle anderen Faktoren gleich bleiben.
Interpretation der kategorischen Variablen (Enthält „SIE HABEN GEWONNEN“): Wenn der Text „SIE HABEN GEWONNEN“ enthält, steigen die Odds von Spam vs. Kein Spam um den Faktor 817% im Vergleich zu E-Mail ohne „SIE HABEN GEWONNEN“ Text, wenn alle anderen Faktoren gleich bleiben.